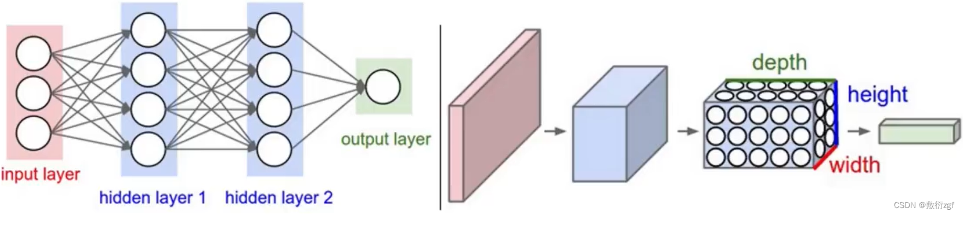
一、CNN与NN的区别

卷积神经网络与传统神经网络的区别：

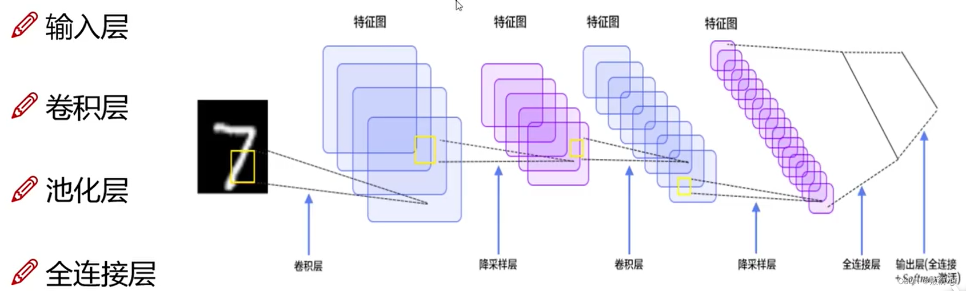
二、CNN的整体架构

1.输入层；2.卷积层；3.池化层；4.全连接层

三、卷积层做了什么

首先将图形分割成一个个小区域，对于每一个区域特征不同；接下来选择一种特征计算的方法，为每一个区域计算特征值，得到特征图。
在图中表现为，深蓝色区域3×3的方格中下标为权重，依次计算每一个3×3的方格的特征值得到最终的绿色特征图。

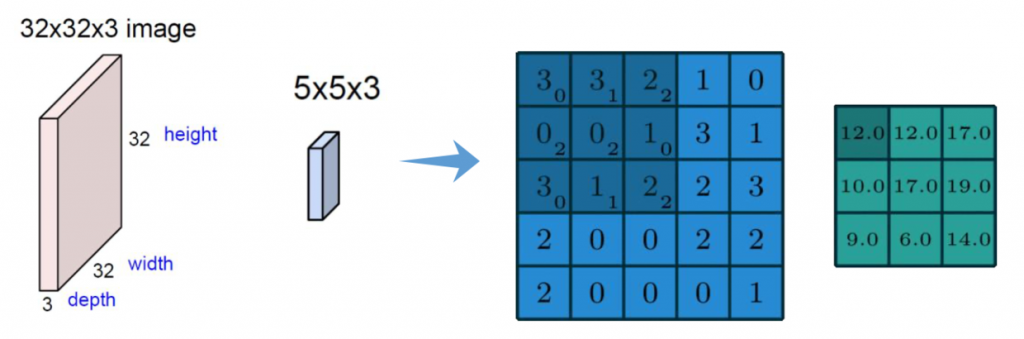
在上图中，输入特征维度是32×32×3，最后一维表示图像颜色通道，在大多数情况下，采用RGB形式。在实际计算过程中，是每一个通道单独计算，将最后的计算结果相加

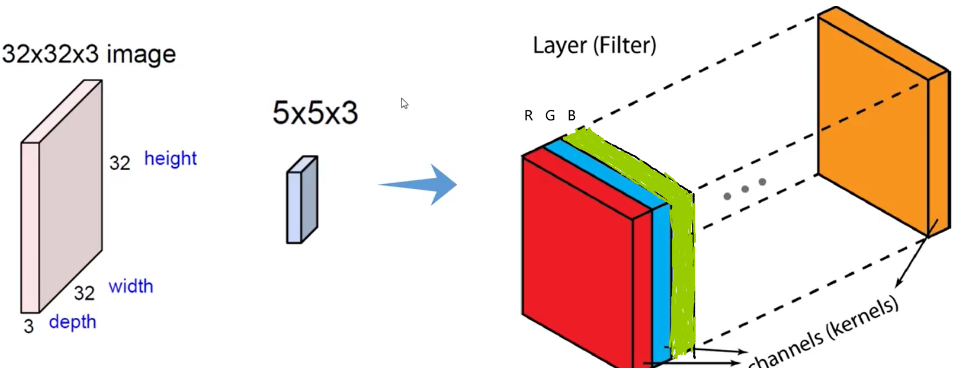
输入为7×7×3，最后一维3表示图像颜色通道，需要注意的是输入的最后一维要和Filter的最后一维保持一致。Filter为3×3×3，那么这里的卷积核大小为3×3，对应输入矩阵中每3×3的大小进行一个区域选择。
计算方式为： 每一个对应位置相乘，最终结果相加，最后不要忘记加上偏置项。

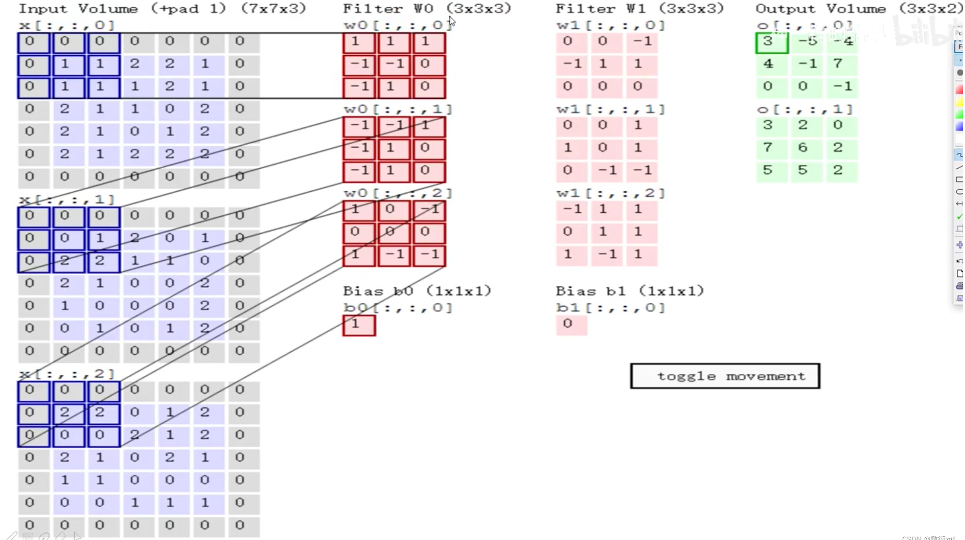
那么并不是卷积一次就完事了，而是可以进行多次卷积，得到若干张特征图，最后进行堆叠。

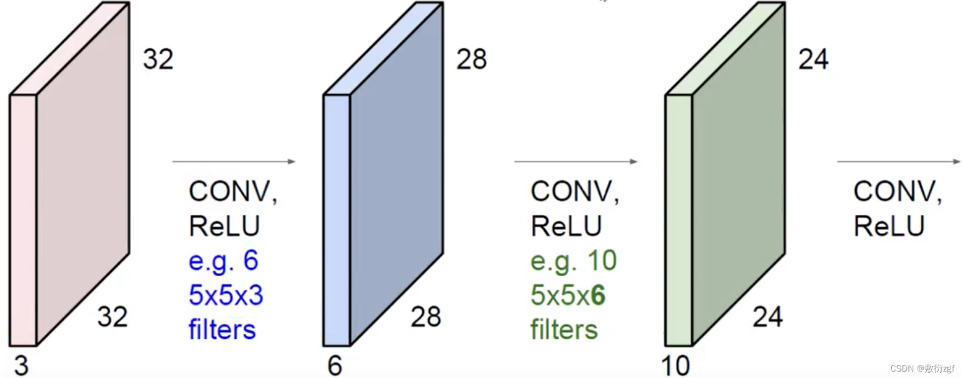
图中首先左侧输入特征维度是32×32×3，经过6个不同的Filter，得到6个特征图进行堆叠；在经过10个不同的Filter，得到10个特征图进行堆叠，依次类推……

（一）卷积层涉及的参数：

1. 滑动窗口步长

（一）卷积层涉及的参数：

1. 滑动窗口步长

从图中可以看出，不同的步长得到的特征图大小也不同。当步长较小时，相当于慢慢的提取特征，细粒度的提取特征，特征提取的较为丰富；当步长较大时，相当于大刀阔斧的提取特征，特征数目较少。

2. 卷积核尺寸
   其实和滑动窗口的尺寸一样，当卷积核尺寸较小时，相当于慢慢的提取特征，细粒度的提取特征，特征提取的较为丰富；当卷积核尺寸较大时，相当于大刀阔斧的提取特征，特征数目较少。
   在一般情况下， 滑动窗口选择1，卷积核尺寸为3×3.

3.边缘填充方法
在滑动窗口移动过程中，我们会发现，有些位置的值被多次计算，那么这些值会对最终的结果影响较大，这样会造成不公平的效果。
解决方法：zero-padding 经过观察发现，越靠近边缘位置的值计算重复越少，越靠近中心位置的值计算次数越多，因此可以在输入特征矩阵外再添加一圈0，使得原本边界的特征被利用的次数增多，在一定程度上弥补了边界信息缺失，边界特征提取不充分的问题。

那么为啥添加的是0 ，而不是其他值呢？ 如果添加其他值则会再计算过程中对最终的结果产生影响。

4.卷积核个数
卷积核个数取决于最终在计算过程中得到多少个特征图，10个特征图也就对应10个卷积核。

（二）卷积层的计算公式：

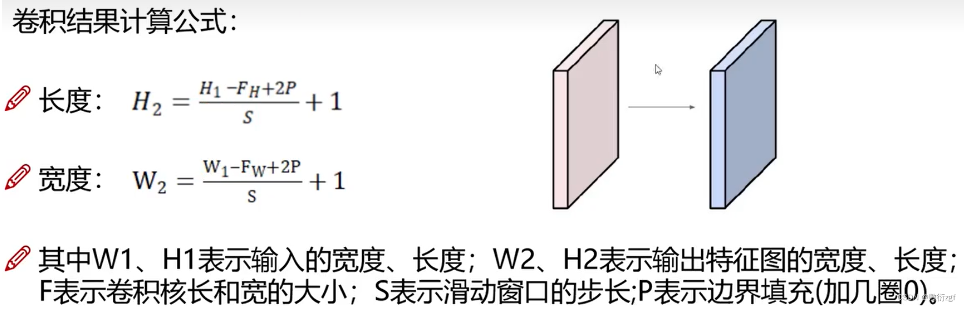
这里需要注意的是边界填充为啥要乘2，原因是我们再输入的特征矩阵周围添加了一圈0，是上下左右都填充了，所以长度和宽度都扩大为原来的两倍。

举个栗子：
如果输入数据是32×32×3的图像，用10个5×5×3的filter来进行卷积操作，指定步长为1，边界填充为2，最终输入的规模是？
利用公式：（32-5+2×2）/ 1 + 1 = 32 ，因此最终的输出规模为：32×32×10
此时我们可以发现：经过卷积操作后，特征并不一定缩小，可以保持特征图长度和宽度不变。

（三）卷积参数共享：
用同样一个卷积核，对图中的每一个小区域进行特征提取。也就是说，对每一个区域进行特征提取时，卷积核中的参数不会发生改变。

如果输入数据依旧是32×32×3的图像，继续用10个5×5×3的filter来进行卷积操作，所需的权重参数个数有多少？
5×5×3 = 75 ，表示一个卷积核需要75个参数，10个卷积核共计750个参数，但每一个卷积核还有一个偏置参数 b ，因此最终只需要 750 + 10 = 760 个参数即可。

四、池化层的作用
在卷积层我们的想法是特征图中的特征越多越好，越多表示特征提取越细腻，能够得到的特征信息越多；但是并不是每一个特征都是有用的，因此池化层的作用就是将得到的特征图进行压缩。

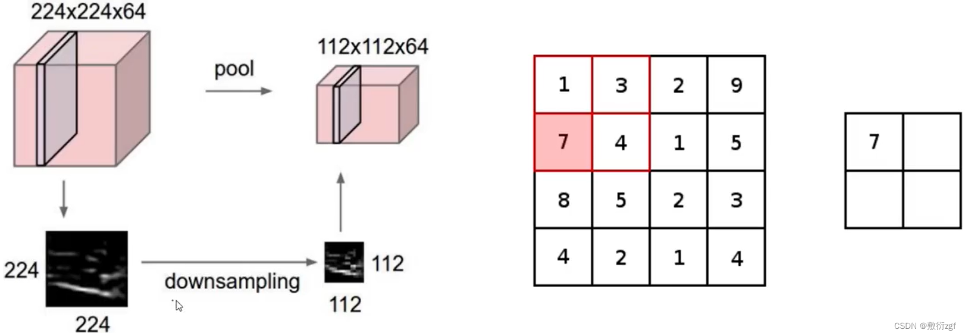
这里需要注意的是：压缩的是每一个特征矩阵的长和宽，并不会压缩特征个数。

压缩方法：最大池化

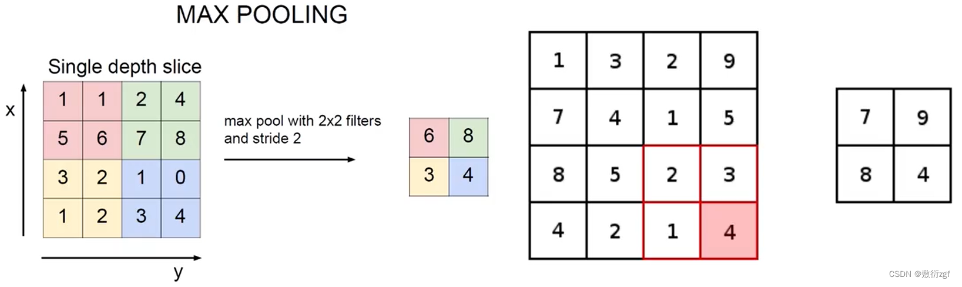
过程是一步一步的移动滑动窗口，找到并取出每一个滑动窗口中的最大值。在池化层中，并没有涉及到任何的矩阵计算，只是进行矩阵筛选、压缩和过滤。

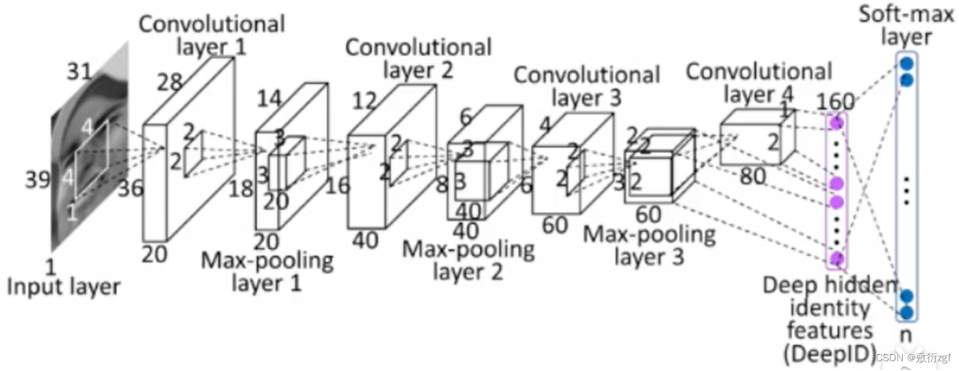
五、卷积神经网络的整体架构
通过观察图，我们发现了几个特点：

首先每一个卷积过后都连接一个Relu激活函数；
每两次卷积后进行一次池化操作；

所有的卷积和池化操作完成后进行全连接FC，
全连接层得到最终的分类结果。

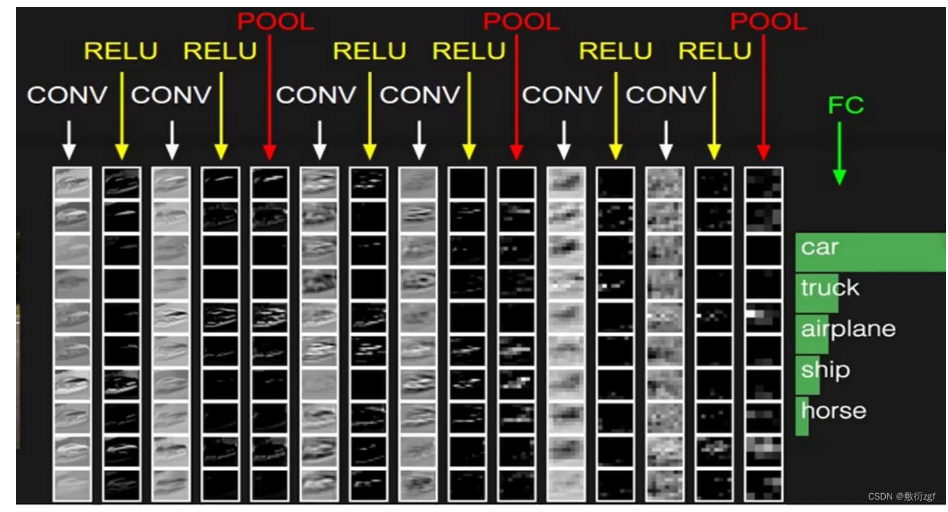
那么我们必须要思考了，卷积和池化操作完成后得到的是一个立体的三维特征图，那么如何进行分类操作呢？
由于全连接层无法连接三维的特征图，因此需要将特征图拉成一维的特征向量。
例如：图中最终进行的是5分类任务，假设卷积和池化操作完成后得到的是一个32×32×10的特征图，将其转换成长度为 10240（32×32×10）的特征向量，连接维度为[10240，5]的全连接层，最终将10240的特征转换为预测的5个类别的概率值。

小Tips： 在计算神经网络层数时，只有带参数计算的才能称为层，因此conv卷积层、FC全连接层带参数计算，上图中为7层卷积神经网络