1、贝叶斯定理
先验概率：即基于统计的概率，是基于以往历史经验和分析得到的结果，不需要依赖当前发生的条件。

后验概率：则是从条件概率而来，由因推果，是基于当下发生了事件之后计算的概率，依赖于当前发生的条件。

条件概率：记事件A发生的概率为P(A)，事件B发生的概率为P(B)，则在B事件发生的前提下，A事件发生的概率即为条件概率，记为P(A|B)。

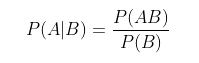
贝叶斯公式：贝叶斯公式便是基于条件概率，通过P(B|A)来求P(A|B)，如下：

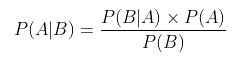
将A看成“规律”，B看成“现象”，那么贝叶斯公式看成：

全概率公式：表示若事件

{A_1},{A_2}, \cdots ,{A_n}

构成一个完备事件组且都有正概率，则对任意一个事件B都有公式成立： 

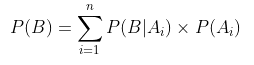
将全概率公式带入贝叶斯公式中，得到：

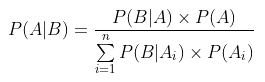
2、朴素贝叶斯算法的原理

特征条件假设：假设每个特征之间没有联系，给定训练数据集，其中每个样本x都包括n维特征，即x = ({x_1},{x_2}, \cdots ,{x_n})，类标记集合含有k种类别，即y = ({y_1},{y_2}, \cdots ,{y_k})。

对于给定的新样本x，判断其属于哪个标记的类别，根据贝叶斯定理，可以得到x属于{y_k}类别的概率P({y_k}|x)：

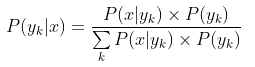
后验概率最大的类别记为预测类别，即：

\mathop {\arg \max }\limits_{​{y_k}} P({y_k}|x)

朴素贝叶斯算法对条件概率分布作出了独立性的假设，通俗地讲就是说假设各个维度的特征

{x_1},{x_2}, \cdots ,{x_n}

互相独立，在这个假设的前提上，条件概率可以转化为：

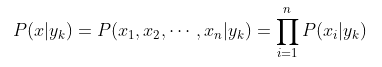
代入上面贝叶斯公式中，得到：

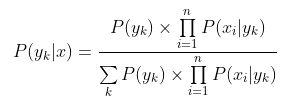
于是，朴素贝叶斯分类器可表示为：

适用范围：
朴素贝叶斯只适用于特征之间是条件独立的情况下，否则分类效果不好，这里的朴素指的就是条件独立。
朴素贝叶斯主要被广泛地使用在文档分类中。
朴素贝叶斯常用的三个模型有：

高斯模型：处理特征是连续型变量的情况。
多项式模型：最常见，要求特征是离散数据。
伯努利模型：要求特征是离散的，且为布尔类型，即true和false，或者1和0。

4、拉普拉斯平滑

为了解决零概率的问题，法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

4、朴素贝叶斯算法的优缺点

优点：

1、朴素贝叶斯模型有稳定的分类效率。
2、对小规模的数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。
3、对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：


1、需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
2、对输入数据的表达形式很敏感（离散、连续，值极大极小之类的）。

5、python代码实现
库方法：sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

其中，alpha：拉普拉斯平滑系数

实验内容：sklearn20类新闻分类，20个新闻组数据集包含20个主题的18000个新闻组帖子。

实验方法：首先，加载20类新闻数据，并进行分割。然后，生成文章特征词，接着，使用朴素贝叶斯分类器进行预估。

代码实现：

# coding:utf-8
 
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
 
 
def naviebayes():
    news = fetch_20newsgroups()
    # 进行数据分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
    # 对数据集进行特征抽取
    tf = TfidfVectorizer()
    # 以训练集当中词的列表进行每篇文章重要性统计['a','b','c','d']
    x_train = tf.fit_transform(x_train)
    print(tf.get_feature_names())
    x_test = tf.transform(x_test)
    # 进行朴素贝叶斯算法的预测
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    mlt.fit(x_train, y_train)
    y_predict = mlt.predict(x_test)
    print("预测的文章类别为:", y_predict)
    # 得出准确率
    print("准确率为:", mlt.score(x_test, y_test))
 
if __name__ == '__main__':
    naviebayes()